Table des matières
Avant internet, nous avions seulement des noms de naissance, des surnoms donnés par les autres, et éventuellement des titres honorifiques. Il fallait être écrivain pour avoir un nom de plume, acteur pour avoir un nom de scène, ou clandestin pour avoir un nom de code.
Maintenant tout le monde a un pseudonyme, qui ne sert pas seulement à être anonyme (dans le sens de séparer ses activités numériques d'une identité « réelle » 1)) mais bien de construire une autre identité, sans considération physique telle que l'âge, le sexe ou la couleur de peau, uniquement basée sur les paroles (qui reflètent donc nos croyances et nos centres d'intérêt) et les créations (notamment artistiques).
J'ai trouvé rapidement mon pseudonyme quand j'ai commencé à naviguer dans les internets, et j'ai fait le choix de mélanger mes deux identités car j'avais le sentiment que l'enseignant-chercheur Yoann Marquer gagnerait à travailler avec le concepteur de jeu Apeiron. Une de ces passerelles est la pédagogie, donc il n'est pas étonnant que j'ai concrétisé cette collaboration avec moi-même notamment sous la forme de ce blog.
Mais trêve de narcissisme 2) et passons au sens du mot et au design du logo.
Le mot

Le logo
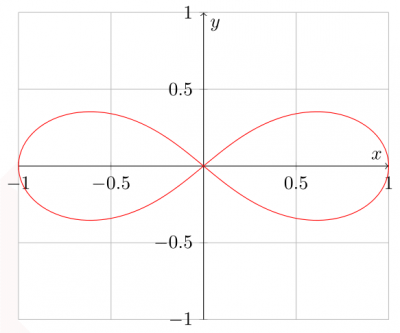
La lemniscate de Bernoulli
Apeiron est un mot désignant l'infini, dont le symbole  a été probablement inspiré par la lemniscate de Bernoulli :
a été probablement inspiré par la lemniscate de Bernoulli :
Pour les curieux, j'utilise le package pgfplots de  pour le rendu. Voici le code utilisé :
pour le rendu. Voici le code utilisé :
\documentclass{standalone}
\usepackage{pgfplots}
\pgfplotsset{every axis/.append style={
axis x line=middle,
axis y line=middle,
axis line style={->,color=black},
xlabel={$x$},
ylabel={$y$},
}}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
xmin=-1,xmax=1,
ymin=-1,ymax=1,
grid=both,
]
\addplot [color=red,domain=0:360,samples=200](
{cos(x)/(1+sin(x)^2)},
{cos(x)*sin(x)/(1+sin(x)^2)}
);
\end{axis}
\end{tikzpicture}
\end{document}
Le code est obtenu à partir de l'équation paramétrique 3) de la lemniscate :
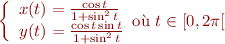
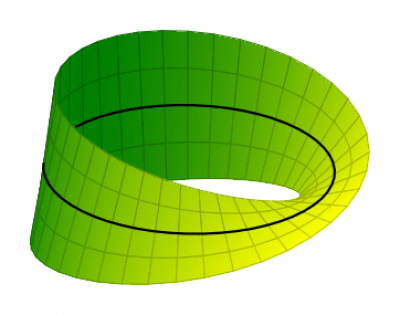
Un objet plat serait très lisible mais trop triste… Or, l'infini est aussi parfois associé au ruban de Möbius, qui est un objet à la fois simple et mystérieux, donc emblématique…
Le ruban de Möbius
Il s'agit cette fois d'un objet en trois dimensions possédant la propriété remarquable de n'avoir qu'une seul face. Vous pouvez en fabriquer un facilement avec du papier, des ciseaux et de la colle comme dans cette vidéo.
Vous pourrez trouver ici une bonne explication de l'équation paramétrique. L'idée est de partir de l'équation paramétrique du cercle :
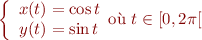
Puis de rajouter un paramètre  , correspondant au fait de faire tourner un bâton sur lui-même pendant que la main qui le fait tourner reste sur la trajectoire du cercle :
, correspondant au fait de faire tourner un bâton sur lui-même pendant que la main qui le fait tourner reste sur la trajectoire du cercle :
![Equation $$\left\{
\begin{array}{r@{}l}
x(t) &{} = (1+\frac{u}{2}\cos \frac{t}{2})\cos t \\
y(t) &{} = (1+\frac{u}{2}\cos \frac{t}{2})\sin t \\
z(t) &{} = \frac{u}{2}\sin \frac{t}{2}\\
\end{array}
\text{où } t \in [0,2\pi[, u \in [-1,1]
\right.$$](/lib/exe/fetch.php?media=wiki:latex:/img90c26d110bd2954317115c6ab353ad90.png)
Notez que si on avait  au lieu de
au lieu de  le ruban serait tourné deux fois sur lui-même, et le ruban aurait alors deux faces comme un ruban normal. Avec cette équation paramétrique nous obtenons la figure suivante :
le ruban serait tourné deux fois sur lui-même, et le ruban aurait alors deux faces comme un ruban normal. Avec cette équation paramétrique nous obtenons la figure suivante :
Cette image a été obtenue avec le code suivant :
\documentclass[border=10pt]{standalone}
\usepackage{pgfplots}
\pgfplotsset{width=7cm,compat=1.8}
% Code written by Jake on TeX.SE.
\begin{document}
\begin{tikzpicture}
\begin{axis}[
hide axis,
view = {40}{40}
]
\addplot3 [
surf,
colormap/greenyellow,
shader = faceted interp,
point meta = x,
samples = 40,
samples y = 5,
z buffer = sort,
domain = 0:360,
y domain =-0.5:0.5
] (
{(1+0.5*y*cos(x/2)))*cos(x)},
{(1+0.5*y*cos(x/2)))*sin(x)},
{0.5*y*sin(x/2)}
);
\addplot3 [
samples=50,
domain=-145:180,
% The domain needs to be adjusted manually,
% depending on the camera angle, unfortunately
samples y=0,
thick
] (
{cos(x)},
{sin(x)},
{0}
);
\end{axis}
\end{tikzpicture}
\end{document}
Le code final
Je voudrais un ruban de Möbius qui s'enroulerait suivant la trajectoire de la lemniscate, et non un cercle. Il suffit donc de reprendre l'équation paramétrique du ruban de Möbius en remplaçant  par
par 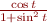 dans
dans 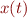 , et
, et  par
par 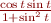 dans
dans 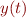 . Nous obtenons donc l'équation paramétrique suivante :
. Nous obtenons donc l'équation paramétrique suivante :
![Equation $$\left\{
\begin{array}{r@{}l}
x(t) &{} = (1+u\cos \frac{t}{2})\frac{\cos t}{1 + \sin^2 t} \\
y(t) &{} = (1+u\cos \frac{t}{2})\frac{\cos t \sin t}{1 + \sin^2 t} \\
z(t) &{} = u\sin \frac{t}{2}\\
\end{array}
\text{où } t \in [0,2\pi[, u \in [-0.5,0.5]
\right.$$](/lib/exe/fetch.php?media=wiki:latex:/img98adea480fe8ef073710ae59416d61d5.png)
Malheureusement, la figure n'est pas très jolie :
Déjà, la largeur du ruban est trop grande, ce qui laisse trop peu d'espace pour voir les espaces centraux. Je la divise donc par deux. Mais surtout le « plat » du ruban est sur le coté, alors que je l'aurais voulu au centre. Cela revient à décaler la progression du bâton tournant de  . Plutôt que de rajouter des constantes, je me suis contenté d'échanger les sinus et cosinus dans la lemniscate :
. Plutôt que de rajouter des constantes, je me suis contenté d'échanger les sinus et cosinus dans la lemniscate :
![Equation $$\left\{
\begin{array}{r@{}l}
x(t) &{} = (1+u\cos \frac{t}{2})\frac{\sin t}{1 + \cos^2 t} \\
y(t) &{} = (1+u\cos \frac{t}{2})\frac{\sin t \cos t}{1 + \cos^2 t} \\
z(t) &{} = u\sin \frac{t}{2}\\
\end{array}
\text{où } t \in [0,2\pi[, u \in [-0.25,0.25]
\right.$$](/lib/exe/fetch.php?media=wiki:latex:/img695aba8e5ba85a73434f19e13153c054.png)
Ah, voilà qui est mieux ! :)
Comme le but est de faire un logo, il reste plusieurs petites choses à faire :
- Rendre les polygones (basés sur des courbes de Bézier) invisibles, pour cela il suffit d'enlever le “faceted” dans les options.
- Personnaliser les couleurs du dégradé. Là encore, c'est assez facile vu les options disponibles. Il suffit de définir les positions de couleurs de référence, et il s'occupe tout seul du dégradé. J'ai choisi bleu-noir-bleu, car le bleu est ma couleur préférée et que le noir au centre m'évoque un trou noir mystérieux là où se produit le repliement du ruban…
- Sur dokuwiki et YouTube les logos sont carrés. Comme je ne souhaite pas déformer l'image, le plus simple est de créer un carré blanc et d'insérer l'image au centre.
- Lisser les courbes. Pour cela il suffit d'augmenter le nombre de points, mais bien sûr cela augmente le temps de compilation. Pour le logo final j'ai poussé
 dans ses derniers retranchements (au dessus il crashe), mais dans le code suivant j'ai gardé une précision assez faible pour que vous puissiez compiler rapidement :
dans ses derniers retranchements (au dessus il crashe), mais dans le code suivant j'ai gardé une précision assez faible pour que vous puissiez compiler rapidement :
\documentclass{standalone}
\usepackage{pgfplots}
\pgfplotsset{width=7cm,compat=1.8}
\begin{document}
\begin{tikzpicture}
\fill[white] (-3,-3) -- (-3,3) -- (3,3) -- (3,-3) -- cycle;
\draw (0,0) node{
\begin{tikzpicture}
\begin{axis}[
hide axis,
view = {0}{60}
]
\addplot3 [
surf,
colormap={nuanceBleu}{color(0cm)=(blue); color(1.5cm)=(black); color(3cm)=(blue)},
shader = interp,
point meta = x,
samples = 40,
samples y = 10,
z buffer = sort,
domain = 0:360,
y domain =-0.25:0.25
] (
{(1+y*cos(x/2)))*sin(x)/(1+cos(x)^2)},
{(1+y*cos(x/2)))*sin(x)*cos(x)/(1+cos(x)^2)},
{y*sin(x/2)}
);
\end{axis}
\end{tikzpicture}
};
\end{tikzpicture}
\end{document}
Et bien sûr vous pouvez voir le résultat final en haut à gauche de la page ^^
La bannière
Je me suis mis en tête de créer une bannière pour ma chaîne voire des cartes de visite, en écrivant “dr Apeiron” avec des symboles mathématiques, un peu dans le style Leet :
- Le premier d pouvait être un “d rond” (comme pour les dérivées partielles) et le A un delta majuscule, ce qui est un hommage à la fois au calcul infinitésimal et à la physique.
- Le i peut être un
 et le o un
et le o un  , en hommage à la calculabilité et à l'informatique. Samae m'a conseillé de les redimensionner4) au même niveau que les autres lettres minuscules pour que le résultat final soit plus agréable à l’œil, et que les chiffres soient écrits en monospace pour faire penser à un terminal.
, en hommage à la calculabilité et à l'informatique. Samae m'a conseillé de les redimensionner4) au même niveau que les autres lettres minuscules pour que le résultat final soit plus agréable à l’œil, et que les chiffres soient écrits en monospace pour faire penser à un terminal. - Osiris m'a suggéré que le n final soit un
 . En plus il y a la “blague” qu'il y a deux r dans le pseudo (
. En plus il y a la “blague” qu'il y a deux r dans le pseudo ( ou
ou 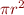 fonctionnent tous les deux dans ce cas). J'aurais préféré un
fonctionnent tous les deux dans ce cas). J'aurais préféré un  , mais c'est vrai que l'hommage à la géométrie est ici tout trouvé…
, mais c'est vrai que l'hommage à la géométrie est ici tout trouvé… - Enfin, je trouvais bon le conseil de Samae d'essayer de glisser mon logo dans ma bannière. Au final cela aurait été illisible, mais en faisant des tests j'ai trouvé comment lier le p et le e pour faire apparaître l'infini, que j'ai mis en bleu pour qu'il reste au milieu du nom noir sur fond blanc.
Au final le résultat est un peu étrange, et j'avoue avoir bricolé comme un sagouin. Mais bon, pour la postérité, voilà mon code final :
\documentclass[tikz]{standalone}
\usepackage{lmodern}
\usepackage[T1]{fontenc}
\usepackage[french]{babel}
\usepackage[utf8]{inputenc}
\usepackage{scalerel}
\usepackage{tikz}
\usepackage{bm}
\newcommand{\baseLine}{0.2 pt}
\newcommand{\hauteur}{1.0}
\newcommand{\largeur}{4.0}
\newcommand{\blankP}{
\begin{tikzpicture}[baseline=\baseLine]
\fill[white, thick] (0,0) rectangle (0.28,0.4);
\end{tikzpicture}
}
\newcommand{\barP}{\mathtt{p}\hspace{-0.309cm}\blankP}
\newcommand{\blankE}{
\begin{tikzpicture}[baseline=\baseLine]
\fill[white, thick] (0,0) rectangle (0.38,0.177);
\fill[white, thick] (0,0.223) rectangle (0.38,0.4);
\end{tikzpicture}
}
\newcommand{\barE}{\mathtt{e}\hspace{-0.43cm}\blankE}
\newcommand{\longBarE}{\barE\hspace{-0.3cm}\barE}
\newcommand{\blueinfty}{\textcolor{blue}{\boldsymbol{\infty}}}
\newcommand{\blankInfty}{\hspace{-0.15cm}
\begin{tikzpicture}[baseline=\baseLine]
\fill[white] (0.3,0.12) rectangle (0.4,0.177);
\end{tikzpicture}
}
\newcommand{\pe}{\barP\hspace{0.075cm}\longBarE\hspace{-0.935cm}\blueinfty\blankInfty}
\newcommand{\sized}[1]{\scalerel*{\mathtt{#1}}{r}}
\begin{document}
\begin{tikzpicture}
\draw[white, thick] (0,0) rectangle (\largeur,\hauteur);
\draw (\largeur/2,\hauteur/2) node[] {\Huge${\partial r\ \Delta \pe \sized{1} r \sized{0} \pi}$};
\end{tikzpicture}
\end{document}