Ceci est une ancienne révision du document !
Table des matières
Cette page regroupe mes anciens projets de recherche, qu'ils soient terminés ou non.
La résolvante de Galois
Versions
Voici notre brouillon s'attardant davantage sur l'histoire des mathématiques.
Voici une synthèse mieux rédigée et focalisée sur la caractérisation du groupe de Galois.
Le projet
Ce que nous appelons aujourd'hui la « théorie de Galois » est l'étude des extensions de corps commutatifs par des « groupes de Galois », c'est à dire les ensembles d'automorphismes d'une extension laissant invariant le corps de base. Cette théorie s'est avérée fertile pour beaucoup de domaines1), mais le degré d'abstraction actuel cache l'extrême simplicité de la théorie initiale.
Mon camarade Raoul Martin et moi avons fait notre projet de première année de master en 2009-2010 sous la direction du professeur Vincent Cossart à l'Université Versailles Saint-Quentin en Yvelines, en étudiant directement le manuscrit de Galois. Le but était double : d'une part en formaliser les résultats avec des notations modernes tout en s'en tenant à la fascinante simplicité de la preuve initiale. D'autre part, à cause de la mort tragique de Galois son manuscrit est resté inachevé, donc nous avons dû reconstruire les preuves manquantes selon les outils disponibles et en essayant de garder l'esprit de la preuve initiale. Notre rapport a été suffisamment apprécié pour que nous soyons invités à parler durant les Journées Mathématiques des 20 ans de l'UVSQ2).
Contexte historique
Le problème initial est de chercher à exprimer les racines d'un polynôme 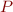 à coefficients dans un corps
à coefficients dans un corps  (par exemple
(par exemple  l'ensemble des rationnels) par une combinaison de fonctions élémentaires\footnote{Addition, soutraction, multiplication, division et les racines carrées, cubiques, etc.} et des coefficients du polynôme. Si cela est possible l'équation
l'ensemble des rationnels) par une combinaison de fonctions élémentaires\footnote{Addition, soutraction, multiplication, division et les racines carrées, cubiques, etc.} et des coefficients du polynôme. Si cela est possible l'équation 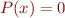 sera dite « résoluble par radicaux ». Par exemple :
sera dite « résoluble par radicaux ». Par exemple :
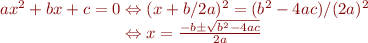
Ainsi, une équation polynomiale du second degré est toujours résoluble par radicaux, comme l'a montré Al-Khwârizmî au IXème siècle. Au XVIème siècle, Tartaglia, Cardano et Ferrari généralisèrent ce résultat aux degrés  et
et  . La question des degrés supérieurs est restée ouverte jusqu'à ce qu'Abel prouve que tous l'équation de degré
. La question des degrés supérieurs est restée ouverte jusqu'à ce qu'Abel prouve que tous l'équation de degré  n'est pas toujours résoluble par radicaux. De façon indépendante, Galois a montré dans son manuscrit un résultat plus général : une équation polynomiale est résoluble par radicaux si et seulement si son groupe de Galois est résoluble.
n'est pas toujours résoluble par radicaux. De façon indépendante, Galois a montré dans son manuscrit un résultat plus général : une équation polynomiale est résoluble par radicaux si et seulement si son groupe de Galois est résoluble.
Esquisse de la preuve
Notre travail a consisté à construire le groupe de Galois en utilisant les outils de Galois.
Soit  le degré du polynôme, et
le degré du polynôme, et  ses racines. Soit
ses racines. Soit 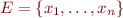 . Nous montrons tout d'abord qu'il existe une application
. Nous montrons tout d'abord qu'il existe une application ![Math $\varphi : E^n \rightarrow K[x_1, \dots, x_n]$](/lib/exe/fetch.php?media=wiki:latex:/img64c83fc176f6f9d3cdc23ed7e7edaf94.png) telle que si
telle que si 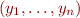 et
et 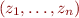 sont des n-uplets distincts de
sont des n-uplets distincts de  , alors
, alors  . L'application
. L'application  est appelée la résolvante de Galois. Nous prouvons que
est appelée la résolvante de Galois. Nous prouvons que 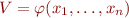 est un élément primitif, c'est à dire que
est un élément primitif, c'est à dire que ![Math $K[V]$](/lib/exe/fetch.php?media=wiki:latex:/imgbd35be96dc7422dc5a79b6b7b92b91e8.png) est un corps et que
est un corps et que ![Math $K[x_1, \dots, x_n] = K[V]$](/lib/exe/fetch.php?media=wiki:latex:/img3cbb6bee98eafcf08e9e7a8cf1503d8d.png) . En particulier, pour tout
. En particulier, pour tout 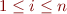 nous avons qu'il existe une fonction rationnelle
nous avons qu'il existe une fonction rationnelle  telle que
telle que 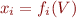 .
.
Soit  le polynôme minimal de
le polynôme minimal de  sur
sur  , et
, et 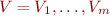 ses racines. Nous prouvons d'une part que pour chacune de ces racines,
ses racines. Nous prouvons d'une part que pour chacune de ces racines, 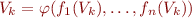 , et d'autre part qu'à
, et d'autre part qu'à  fixé,
fixé, 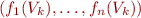 est une permutation des racines de
est une permutation des racines de 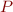 . Donc, pour chaque
. Donc, pour chaque 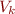 il existe une permutation
il existe une permutation  telle que
telle que 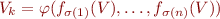 . Nous définissons donc le groupe de Galois par :
. Nous définissons donc le groupe de Galois par :
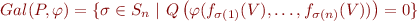
Nous montrons, d'une part que le groupe de Galois est bien un groupe, et d'autre part qu'il est le plus grand groupe vérifiant que pour tout ![Math $F \in K[X_1, \dots, X_n]$](/lib/exe/fetch.php?media=wiki:latex:/img3942b2a277316a09fbddfe7fae26ff61.png) , si
, si 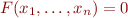 alors
alors 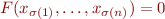 . Ainsi,
. Ainsi, 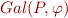 ne dépend que de
ne dépend que de 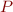 . C'est bien le groupe de Galois associé à l'extension où l'on a ajouté les racines de
. C'est bien le groupe de Galois associé à l'extension où l'on a ajouté les racines de 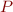 .
.
Réalisabilité classique
Durant ma deuxième année de master Logique Mathématique et Fondements de l'Informatique en 2011, je profitais de ma présence à l'Université Paris-Diderot pour faire mon stage auprès du professeur émérite Jean-Louis Krivine. Il m'avait impressionné par sa démarche tentant d'associer un contenu calculatoire à tous les résultats mathématiques, et il m'a fait travailler sur son article traitant de réalisabilité classique.
La logique intuitionniste peut être vue comme la logique classique où des règles équivalentes comme le tiers exclu, l'élimination de la double négation ou la loi de Peirce ne seraient plus toujours autorisées. La correspondance de Curry-Howard permet d'associer à chaque preuve en logique intuitionniste un programme en lambda-calcul. En cherchant à typer une instruction de contrôle dans un langage dérivant du lambda-calcul, l'informaticien Tim Griffin associa un programme (la commande  ) à la loi de Peirce.
) à la loi de Peirce.
Projets de thèse
Système T avec opérateurs de contrôle
Un des buts est d'étendre le lambda-calcul afin d'étendre la correspondance de Curry-Howard. La réalisabilité classique de Krivine ainsi que le  -calcul de Parigot sont des avancées indépendantes dans cette direction. D'autres tentatives (par Nakano, Sato ou Kameyama par exemple) insistent sur l'aspect non-déterminisme de ces opérateurs de contrôle. Pour forcer le déterminisme, il faut forcer la stratégie d'évaluation, ce que nous faisons avec un lambda-calcul monadique où seules les valeurs (variables ou abstractions) peuvent être argument d'une réduction.
-calcul de Parigot sont des avancées indépendantes dans cette direction. D'autres tentatives (par Nakano, Sato ou Kameyama par exemple) insistent sur l'aspect non-déterminisme de ces opérateurs de contrôle. Pour forcer le déterminisme, il faut forcer la stratégie d'évaluation, ce que nous faisons avec un lambda-calcul monadique où seules les valeurs (variables ou abstractions) peuvent être argument d'une réduction.
Afin d'inclure les entiers et la récurrence, c'est le système T de Gödel et non le lambda-calcul qui sera utilisé comme base. Nous obtenons donc un système T par valeur, que nous traduisons vers un système T « nommé » avec des  , puis vers le système T habituel. En montrant la compatibilité de notre traduction avec la réduction habituelle, nous obtenons la normalisation forte de notre système de calcul en la dérivant de celle du système T.
, puis vers le système T habituel. En montrant la compatibilité de notre traduction avec la réduction habituelle, nous obtenons la normalisation forte de notre système de calcul en la dérivant de celle du système T.
L'idée aurait été ensuite d'ajouter à notre système de calcul des opérateurs de contrôle comme  ,
,  ou
ou  , mais le départ de Tristan Crolard mit le projet en sommeil. Voici ma dernière version de travail.
, mais le départ de Tristan Crolard mit le projet en sommeil. Voici ma dernière version de travail.
Contenu algorithmique des stratégies du lambda-calcul
Les EMAs ont été développées notamment par Serge Grigorieff et Pierre Valarcher dans leur article. L'idée est que certes les Abstract State Machines de Gurevich peuvent simuler étape par étape toutes les machines usuelles3), mais que simulation n'est pas identification. Ainsi, Serge Grigorieff et Pierre Valarcher montrent que des classes naturelles d'EMAs peuvent être littéralement identifiées à ces machines, ce qui fait des EMAs un modèle mathématique unificateur.
Dans cette optique, j'ai cherché à formaliser sous forme de machines abstraites les différentes stratégies d'évaluation contextuelle utilisées pour le lambda-calcul. Le terme à évaluer n'est donc qu'une entrée, et c'est la stratégie d'évaluation elle-même qui est vue comme un algorithme. Les différentes stratégies étudiées sont l'appel par nom, l'appel par besoin et l'appel par valeur, qui sont respectivement implémentées par la machine de Krivine et deux machines créées pour l'occasion :
![Equation $$\begin{array}{r|l@{}c@{}r@{}rcl@{}c@{}r@{}rc}
\text{appel par nom}
&{} \mu &{}\ \star\ &{} (t_1)t_2 \ \star\ &{} \pi &{} \succ &{} \mu, \mathunderscore &{}\ \star\ &{} t_1 \ \star\ &{} t_2,\pi \\
&{} \mu, \mathunderscore &{}\ \star\ &{} \lambda x.t_1 \ \star\ &{} t_2,\pi &{} \succ &{} \mu &{}\ \star\ &{} t_1[t_2/x] \ \star\ &{} \pi \\
\hline
\text{appel par valeur}
&{} \mu &{}\ \star\ &{} (t_1)t_2 \ \star\ &{} \pi &{} \succ &{} \mu, t_1 &{}\ \star\ &{} t_2 \ \star\ &{} \mathunderscore,\pi \\
&{} \mu, t &{}\ \star\ &{} v \ \star\ &{} \mathunderscore,\pi &{} \succ &{} \mu, \mathunderscore &{}\ \star\ &{} t \ \star\ &{} v, \pi \\
&{} \mu, \mathunderscore &{}\ \star\ &{} \lambda x.t \ \star\ &{} v,\pi &{} \succ &{} \mu &{}\ \star\ &{} t[v/x] \ \star\ &{} \pi \\
\hline
\text{appel par besoin}
&{} \mu &{}\ \star\ &{} (t_1)t_2 \ \star\ &{} \pi &{} \succ &{}\mu, \mathunderscore &{}\ \star\ &{} t_1 \ \star\ &{} t_2,\pi \\
&{} \mu, \mathunderscore &{}\ \star\ &{} v \ \star\ &{} t, \pi &{} \succ &{} \mu, v &{}\ \star\ &{} t \ \star\ &{} \mathunderscore,\pi \\
&{} \mu, \lambda x.t &{}\ \star\ &{} v \ \star\ &{} \mathunderscore,\pi &{} \succ &{} \mu &{}\ \star\ &{} t[v/x] \ \star\ &{} \pi \\
\end{array}$$](/lib/exe/fetch.php?media=wiki:latex:/img23ea47b2a57ca55b74b12841a5854a84.png)
Nous prouvons que nos machines sont correctes, c'est à dire que si un terme est évalué avec une stratégie jusqu'à une valeur finale en  substitutions, alors la machine ne contenant que ce terme4) fait des transitions jusqu'à arriver à la même valeur en ayant fait exactement
substitutions, alors la machine ne contenant que ce terme4) fait des transitions jusqu'à arriver à la même valeur en ayant fait exactement  substitutions puis s'arrête. Puis nous traduisons ces machines sous forme d'EMA, et discutons des généralisations possibles.
substitutions puis s'arrête. Puis nous traduisons ces machines sous forme d'EMA, et discutons des généralisations possibles.
Voici la dernière version.

 et la pile
et la pile  sont vides.
sont vides.