Table des matières
Introduction
Une langue construite (en anglais conlang) diffère des langues naturelles par le fait qu'elle soit conçue de façon plus ou moins planifiée (le kobaïen est une exception notable), mais surtout par une ou quelques personnes et dans un temps relativement court. Plusieurs raisons peuvent pousser la création d'une langue, que ce soit pour fournir une langue internationale (comme l'espéranto), étayer un univers de fiction (comme le travail monumental de Tolkien) ou juste pour le plaisir.
Mon intérêt pour les langues m'est venu quand j'ai découvert la cryptographie tout gosse, et que je me disais que si j'arrivais à enseigner à un ami une langue créée pour l'occasion personne ne pourrait nous comprendre. C'était stupide pour trois raisons :
- L'enseignement de cette langue doit passer par un canal sécurisé, sinon « l'ennemi » pourra l'apprendre aussi. Certes, il n'y a besoin que dans un investissement de secret au départ, mais dans le fond ça ne fait que reporter le problème.
- Les langues sont structurées donc il est possible de les analyser dès lors qu'on dispose d'un échantillon assez gros. C'est d'ailleurs un travail fascinant (voir par exemple le cas du linéaire A).
- C'était négliger la quantité de travail nécessaire par rapport au but recherché, surtout quand j'ai fini par en apprendre davantage sur le cryptage. En passant, voici un lien utile sur l'auto-défense numérique, qui n'est pas superflu en ces temps de surveillance.
Malgré cela, l'idée de créer ma propre langue est restée en moi, déjà comme outil pour me poser des questions sur les langues. Le français est ma langue maternelle, j'ai appris l'anglais, l'espagnol et le latin à l'école, l'allemand et le grec ancien par correspondance, et j'ai commencé à bouquiner des articles de linguistique dès que j'ai compris que ça existait en ligne. Plus tard mon intérêt pour la mathématique, la logique puis la conception de jeux est venu nourrir cette envie, pendant que mes parties de jeux de rôle me donnèrent envie de donner corps à l'univers que j'avais en tête, et surtout à la façon de penser de ses habitants.
L'Ancien
Ainsi, pour moi cette langue est à la fois une façon de tester des principes, mais aussi une façon d'étayer un univers de fiction. Dans cette histoire, un peuple appelé les Anciens a réussi à créer des passages reliant des Terres parallèles, aussi ils utilisent une version simplifiée de leur langue comme lingua franca.
Plus précisément, le Haut-Ancien est un langage parlé uniquement par les Anciens entre eux. Il s'agit d'un langage formel, qui englobe énormément de structures et nuances, signes de leur façon d'appréhender le monde. Cela est dû à la fois au fait qu'ils sont issus originellement d'un univers artificiel1), et qu'ils ont incorporé dans leur vision du monde quotidienne énormément de connaissances sur le fonctionnement des mondes et des gens. Aucun Ancien d'ailleurs ne sait parler tout le Haut-Ancien, car ils l'apprennent au fur et à mesure au fil de leurs études. On peut d'ailleurs voir le Haut Ancien comme une continuité cohérente de jargons spécialisés. Mais tous maitrisent la langue pour l'utilisation quotidienne, et tous les adultes qui sont revenus ont les connaissances nécessaires liées au Voyage entre les mondes.
L'Ancien dont nous parlons ici n'est pas le Haut-Ancien mais une langue artificielle inspirée du Haut-Ancien quoique considérablement simplifiée, qui a été conçue pour servir de langue commune entre les mondes. Cela explique l'accent mis sur la régularité et la simplicité recherchée de la langue. Même du temps des Anciens, il y a eu une opposition entre l'Ancien classique qui est utilisé pour le commerce, les chants, et le théâtre, et les différents parlers locaux. On parle de différents Anciens « communs » ou « vulgaires » (selon sa classe sociale) qui ont été obtenus par un accès partiel à l'Ancien classique de populations locales n'utilisant par les mêmes langues entre elles et utilisant donc une version locale de l'Ancien de façon à se comprendre, tout en empruntant des mots et des structures aux langues locales. Après la Chute des Anciens, ces pidgins sont devenus des créoles ayant tous l'Ancien comme racine mais pouvant différer énormément d'une région à une autre, l'Ancien classique pouvant continuer à être utilisé par des élites, en particulier celles ayant accès à l'écriture. En particulier après la Chute, l'Ancien a donc eu un rôle similaire au latin durant le Moyen-Âge.
Principes
Le but est de créer une langue basée sur l'apprentissage de peu de racines qui se combinent pour donner tous les mots communs. Pour faciliter l'apprentissage et la combinatoire, ce sera une langue isolante. Afin de faciliter l'identification des concepts, je voudrais qu'une racine corresponde à une syllabe. Ainsi, nous aurions des motifs de la forme :
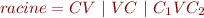
où les V sont des voyelles et les C des consonnes. Par exemple, « la » est de la forme CV alors que « poc » est de la forme CVC.
Le problème avec ces motifs est qu'il peut y avoir confusion. Par exemple, comment distinguer « la-poc » de « lap-oc » ? Ou à l'oreille, comment distinguer « la-ac » de « lac » ou « poc-ca » de « po-ca » ? Une (mauvaise) solution serait d'admettre l'ambiguïté ou de compter sur des finesses comme des sons longs qui déforment l'ensemble de la phrase.
Une autre solution serait de n'admettre que les racines de la forme  (ou
(ou  mais qui est moins naturel), mais dans ce cas on aurait moins de racines (ce qui certes facilite l'apprentissage) et il serait logique de basculer vers un syllabaire, qui implémenterait rigoureusement la notion de « un symbole = une racine ». Ce qui serait une très bonne chose, car dans ce cas même si la langue parlée n'a aucune rapport avec la langue écrite les scripteurs pourraient s'en servir comme idéogrammes (exemple de la Chine).
mais qui est moins naturel), mais dans ce cas on aurait moins de racines (ce qui certes facilite l'apprentissage) et il serait logique de basculer vers un syllabaire, qui implémenterait rigoureusement la notion de « un symbole = une racine ». Ce qui serait une très bonne chose, car dans ce cas même si la langue parlée n'a aucune rapport avec la langue écrite les scripteurs pourraient s'en servir comme idéogrammes (exemple de la Chine).
Toutefois je souhaitais plutôt partir sur un abécédaire afin de maintenir l'idée de décomposition d'une racine en éléments syntaxiques mais non sémantiques2) et surtout pour avoir davantage de racines sans avoir à utiliser trop de sons étranges. Pour régler le problème précédent il faut donc un séparateur.
Pour distinguer « la-poc » de « lap-oc » nous utilisons le phénomène naturel du voisement (celui qui explique pourquoi nous disons « anegdote » et non « anecdote »). Ainsi, le 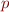 se voise en
se voise en  donc nous aurions d'une part « lapoc » et de l'autre « laboc ». Dans un motif
donc nous aurions d'une part « lapoc » et de l'autre « laboc ». Dans un motif  c'est la première consonne qui se voise, ainsi il suffit de restreindre les consonnes terminant une syllabe aux consonnes qui peuvent se voiser (que je noterais
c'est la première consonne qui se voise, ainsi il suffit de restreindre les consonnes terminant une syllabe aux consonnes qui peuvent se voiser (que je noterais  ), et elles se voiseront effectivement si la syllabe qui suit (d'un même mot ou d'un autre mot d'une même phrase ?) est une voyelle ou la même consonne.
), et elles se voiseront effectivement si la syllabe qui suit (d'un même mot ou d'un autre mot d'une même phrase ?) est une voyelle ou la même consonne.
C'est par assimilation phonétique qu'une consonne suivie d'une voyelle se voise (puisqu'une voyelle est toujours voisée, sauf si chuchotée) ? En fait toujours voiser la deuxième consonne d'une racine, sauf si fin du mot ? Par exemple je trouve tegpa plus joli (plus coulant en bouche) que tekpa, et avso plutôt qu'afso.
En tout cas, par dissimilation quand deux consonnes identiques se suivent, il vaut mieux que la première mute (se voiser serait trop proche). Je propose d'utiliser les consonnes ne pouvant pas se voiser et donc n'entrainant pas d'ambiquité. Par rapprochement sur la table de l'API, ça donnerait ap-pa → ampa, af-fa → amfa, at-ta → anta, ak-ka → anka, as-sa → ansa, ach-cha → ancha, arh-rha → anrha. Et donc en fait des nasales peuvent apparaître dans les dialectes dérivés.
Il ne reste qu'un cas à examiner : faire la distinction si les deux mêmes voyelles se suivent. En fait, le plus simple et le plus agréable (pour un occidental) à l'oreille consiste à éliminer systématiquement les hiatus, en intercalant par exemple un « h » (le h aspiré).
En passant, il y a bien un inconvénient à utiliser le voisement : une version voisée ou non voisée d'un son sont assimilées à la même consonne. Ainsi, 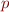 et
et  sont considérés comme la même lettre, ce qui réduira le nombre de racines possibles. De plus, utiliser le
sont considérés comme la même lettre, ce qui réduira le nombre de racines possibles. De plus, utiliser le  pour éliminer les hiatus la retire également des consonnes possibles. Toutefois il est possible de gagner des racines en élargissant les motifs, par exemple
pour éliminer les hiatus la retire également des consonnes possibles. Toutefois il est possible de gagner des racines en élargissant les motifs, par exemple  où
où  est une consonne comme
est une consonne comme 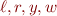 , par exemple « clé » ou « bio ».
, par exemple « clé » ou « bio ».
Toutefois, il faut se rappeler que ce genre de subtilités est courant en Occident, mais pas forcément ailleurs dans le monde. Par exemple, la prononciation de mots occidentaux par un japonnais montre à quel point notre système est peu compatible avec le sien. Ainsi, je vais me contenter de garder cette possibilité sous le coude, et en attendant d'en avoir besoin de me contenter des motifs les plus simples possibles.
Phonologie
Les racines sont de la forme :
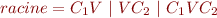
- Le h est rajouté entre deux voyelles.
Je suis un peu triste de noter  et
et 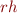 en deux lettres mais tout autre choix rendrait la lecture plus difficile, d'autant plus que je poserai la graphie plus tard. J'ai bien conscience d'avoir fait mes choix en m'inspirant (trop3)) fortement du français4), mais c'est une base de laquelle partir. D'ailleurs, je précise que comme en français les tons ne servent qu'à marquer la ponctuation (à préciser) et qu'il n'y a pas de voyelles/consonnes courtes/longues (hormis pour marquer l'insistance à l'oral).
en deux lettres mais tout autre choix rendrait la lecture plus difficile, d'autant plus que je poserai la graphie plus tard. J'ai bien conscience d'avoir fait mes choix en m'inspirant (trop3)) fortement du français4), mais c'est une base de laquelle partir. D'ailleurs, je précise que comme en français les tons ne servent qu'à marquer la ponctuation (à préciser) et qu'il n'y a pas de voyelles/consonnes courtes/longues (hormis pour marquer l'insistance à l'oral).
A propos, il y a sept voyelles :
- et des voyelles qui s'altèrent si elles sont suivies par une consonne (le séparateur
 excepté) :
excepté) :
Cette altération est une survivance de sons présents en Haut-Ancien, et dans la plupart des mondes l'altération est peu appliquée ou pas du tout, en particulier pour  et
et  et dans une moindre mesure pour
et dans une moindre mesure pour  . Toutefois, nous décrivons ici l'Ancien classique, qui pourra sembler nécessaire si vous avez à faire à des élites, mais qui semblera ampoulé si vous avez à faire à des gens du commun.
. Toutefois, nous décrivons ici l'Ancien classique, qui pourra sembler nécessaire si vous avez à faire à des élites, mais qui semblera ampoulé si vous avez à faire à des gens du commun.
Ainsi, nous avons 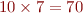 racines de la forme
racines de la forme  ,
, 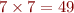 racines de la forme
racines de la forme  , et
, et  racines de la forme
racines de la forme  , soit un total de 609 racines, théoriquement. Évidemment, toutes les combinaisons ne sont pas utilisées, et certaines le sont plus fréquemment que d'autres.
, soit un total de 609 racines, théoriquement. Évidemment, toutes les combinaisons ne sont pas utilisées, et certaines le sont plus fréquemment que d'autres.
Comme il n'y a pas ambiguité, on peut ajouter aussi les  comme mot grammatical, par exemple
comme mot grammatical, par exemple  pour marquer la négation. L'idée est que plus une racine est courante moins elle est longue : une lettre pour les mots grammaticaux,
pour marquer la négation. L'idée est que plus une racine est courante moins elle est longue : une lettre pour les mots grammaticaux,  pour les racines courantes,
pour les racines courantes,  pour les racines grammaticales (temps, cas, sauf nombre ? etc.), et trois pour les rares.
pour les racines grammaticales (temps, cas, sauf nombre ? etc.), et trois pour les rares.
L'écriture
L'ancien classique est un système alphabétique cursif formant ses racines de gauche à droite, puis combinant ses racines de haut en bas pour former des mots et des phrases. Il existe une version calligraphique pouvant être utilisée par les administrations non mécanisées (les Anciens ont démocratisé l'usage du papier, qui est devenu plus rare après la Chute) mais aussi deux versions pour l'imprimerie. La version alphabétique est destinée aux peuples utilisant couramment l'Ancien classique ou des parlers locaux proches. En particulier des variations phonétiques (comme le fait d'altérer ou non une voyelle) n'ont pas d'impact sur le système écrit qui est donc compatible. En raison du caractère fortement isolant de l'Ancien, les racines peuvent être également utilisées de façon idéographiques par les peuples dont la langue a trop dérivé de l'ancien classique. Ainsi, comme en Chine, des locuteurs peuvent avoir un parler différent mais se comprendre par l'écrit. Ces deux versions ont tendance à être mutuellement lisibles, et sont couramment utilisées pour la littérature, l'administration, et les monuments (comme les Passages).
Quelques idées à piocher de notre monde ? J'ai trouvé très intéressantes les orientations du syllabaire inuktitut, le rôle des voyelles dans alphasyllabaire devanagari, ainsi que la notation phonétique très structurée du hangeul coréen.
La numération
Les Anciens comptent en base 12, car 12 a beaucoup de diviseurs, ce qui permet de compter plus facilement et de faciliter les conversions d'un système numérique à un autre. Un mouvement8) a d'ailleurs existé pour faire passer le système à la base 60 (comme chez nous les Babyloniens), mais il a été estimé qu'il était raisonnable de faire apprendre 12 chiffres par cœur mais pas une soixantaine, et la possibilité de compter sur ses phalanges en base 12 a favorisé l'essor du système parmi les marchands et les scribes.
Le nom des chiffres est une application du théorème des restes chinois. Un chiffre est une racine de la forme  où :
où :
 est
est 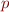 si le chiffre vaut
si le chiffre vaut  modulo
modulo 
 est
est  si le chiffre vaut
si le chiffre vaut  modulo
modulo 
 est
est  si le chiffre vaut
si le chiffre vaut  modulo
modulo 
 est
est  si le chiffre vaut
si le chiffre vaut  modulo
modulo 
 est
est  si le chiffre vaut
si le chiffre vaut  modulo
modulo 
 est
est  si le chiffre vaut
si le chiffre vaut  modulo
modulo 
 est
est  si le chiffre vaut
si le chiffre vaut  modulo
modulo 
Ainsi, les chiffres en Ancien sont : 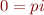 ,
, 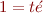 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 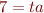 ,
,  ,
,  ,
, 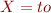 ,
,  . Le
. Le  (pour dix, en chiffres romains) et
(pour dix, en chiffres romains) et  (pour onze, en anglais9)) viennent du journal de la Dozenal Society. En fait, je devrais utiliser le
(pour onze, en anglais9)) viennent du journal de la Dozenal Society. En fait, je devrais utiliser le  et le
et le  inversés mais je les trouve confusants…
inversés mais je les trouve confusants…
Cette notation facilite l'apprentissage des tables d'addition et de multiplication, puisque ces opérations sont compatibles avec l'arithmétique modulaire. Pour prendre un exemple, ![Math $2 + 3 = ko + pa = 2[3]2[4] + 0[3]3[4] = (2+0)[3](2+3)[4] = 2[3]1[4] = ké = 5$](/lib/exe/fetch.php?media=wiki:latex:/imgfb447dd575ac66612e6c7a648f6fe37c.png) . Note : cela aide en donnant le dernier chiffre, mais pas la retenue. Par contre cela n'aide pas du tout pour les comparaisons, raison pour laquelle l'ordre des chiffres doit être appris par cœur (il y a des comptines pour ce faire). De plus, il est possible que la ressemblance des sons pour les différents chiffres cause des problèmes pour certains dyslexiques.
. Note : cela aide en donnant le dernier chiffre, mais pas la retenue. Par contre cela n'aide pas du tout pour les comparaisons, raison pour laquelle l'ordre des chiffres doit être appris par cœur (il y a des comptines pour ce faire). De plus, il est possible que la ressemblance des sons pour les différents chiffres cause des problèmes pour certains dyslexiques.
Pour le reste, la numération des Anciens est un système à notation positionnelle comme notre système décimal ou le binaire, si ce n'est qu'il utilise la base 12. Comme chez nous, les nombres sont écrits par paquets de trois (les milliers, les millions, etc.), mais ils sont aussi prononcés comme tels. Par exemple 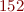 ne se dira pas « cent quarante-deux » mais « un-cinq-deux ». Les paquets sont notés
ne se dira pas « cent quarante-deux » mais « un-cinq-deux ». Les paquets sont notés  où
où  est le numéro du paquet et
est le numéro du paquet et 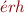 la racine pour « quantité ». Par exemple
la racine pour « quantité ». Par exemple 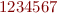 sera littéralement « un million deux-trois-quatre milliers cinq-six-sept », c'est à dire « té kohèrh kopati téhèrh képota ». Les unités se disent « pihèrh » mais elles sont rarement dites (sauf en cas de nombre à virgule). Il est plus accepté de préciser quels sont les objets comptés (dix chaises, onze tables), ou de ne rien dire (pour des nombres abstraits). « pihèrh » est utilisé plutôt dans le cas d'objets physiques indéterminés, par exemple pour des registres.
sera littéralement « un million deux-trois-quatre milliers cinq-six-sept », c'est à dire « té kohèrh kopati téhèrh képota ». Les unités se disent « pihèrh » mais elles sont rarement dites (sauf en cas de nombre à virgule). Il est plus accepté de préciser quels sont les objets comptés (dix chaises, onze tables), ou de ne rien dire (pour des nombres abstraits). « pihèrh » est utilisé plutôt dans le cas d'objets physiques indéterminés, par exemple pour des registres.
Enfin, pour les nombres à virgules on rajoute tout simplement la racine signifiant « négatif » pour noter les puissances après la virgule.
Réflexions
La possession est distinguée entre l'identité (mes souvenirs) et le lien (mes amis), la propriété exclusive (mes chaussures) surtout d'usage, et la propriété commune (les connaissances, le puits du village, etc.). Le nombre n'est pas marqué grammaticalement, à la place des numéros (en base douze) sont utilisés. Les racines ne sont pas distinguées en catégories (nom, verbe, adjectif, …), c'est le suffixe qui détermine le type (chaussure-objet = chaussure, chaussure-personne = cordonnier). Le temps n'est pas marqué non plus, à la place des modaux sont utilisés comme en anglais (je souvenir manger = j'ai mangé). Forme SVO par défaut, bien que cela puisse évoluer selon le mot sur lequel on veut insister (le rôle est porté par des suffixes ou des pronoms). Les « évidentiels » marquent le degré de certitude : rumeur/sagesse populaire/tradition/conte < témoignage < anecdote < expertise (étude) < consensus (réplications), ils sont obligatoires et marquent le début d'une phrase. Usage des factitifs (comme “faire mourir” au lieu de tuer et “faire voir” au lieu de montrer) ? L'impératif n'existe pas dans cette langue (limitée à “je voudrais que tu…”) ? Pas de forme de politesse (liée à la hiérarchie) ni de genre. A priori, vu le RP, pas d'emprunt à part du Haut-Ancien ?
Liens utiles
Dans sa vidéo Vulgarizators, Linguisticae parle du toki pona, une langue minimale qui pourrait servir de source d'inspiration.
Sténographies intéressantes : Duployan shorthand, Gregg shorthand.
Évolution de la phonologie en germanique : loi de Grimm.
 ou un
ou un  .
. , où
, où  aurait été
aurait été 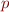 ,
,  ,
,  ,
, 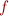 ,
,  si le reste modulo
si le reste modulo  avait été
avait été  ,
,  ,
,  ,
,  ,
,  . Vu la popularité du système en base 12 et qu'Istalis était la capitale du Multivers des Anciens, les historiens soupçonnent que la base
. Vu la popularité du système en base 12 et qu'Istalis était la capitale du Multivers des Anciens, les historiens soupçonnent que la base  était utilisée en Haut-Ancien et que le mouvement rigoriste souhaitait en fait homogénéiser le système commun avec les archives de l'université.
était utilisée en Haut-Ancien et que le mouvement rigoriste souhaitait en fait homogénéiser le système commun avec les archives de l'université.
 est un
est un  est le son dans « jeune ».
est le son dans « jeune ». est le son dans « cône ».
est le son dans « cône ». est le son dans « pâte ».
est le son dans « pâte ».