Ceci est une ancienne révision du document !
Table des matières
Introduction
Il y a beaucoup à dire historiquement sur le sujet, et je referai probablement l'article après l'avoir croisé avec des articles intéressants comme Sciences étonnantes ou Science4All, et surtout il faudrait que je lise l'ouvrage de référence de Hardy. Mais pour l'instant je souhaitais juste mettre au propre mes premières réflexions sur le sujet…
Je vais partir du principe que les sommes infinies comme
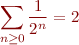
ne vous font pas peur. Si c'est bien le cas, vous savez alors qu'ont dit qu'une somme  est dite convergente si la suite des sommes partielles est finie :
est dite convergente si la suite des sommes partielles est finie :
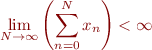
C'est le cas par exemple de 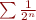 , puisque :
, puisque :
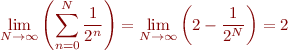
Astuce : le calcul entre parenthèses est obtenu de façon générale pour toutes les séries géométriques, c'est à dire les séries de la forme 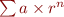 :
:

 est un coefficient
la raison
est un coefficient
la raison  de la suite
de la suite
Principes
Prenons l'exemple des séries géométriques
