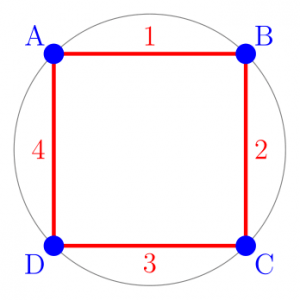
Un polygone (du plan) est dit régulier si tous ses côtés ont la même longueur et tous ses angles ont la même valeur. Par exemple, un triangle équilatéral est régulier mais pas un triangle rectangle, et un carré est régulier contrairement à un rectangle ou un losange.

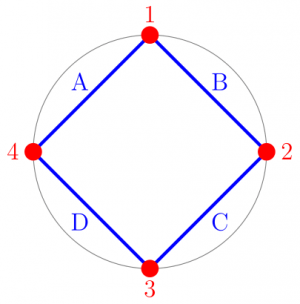
Les polygones réguliers vérifient des propriétés de symétrie qui les rendent « jolis », par exemple ils peuvent être inscrits dans un cercle, et en tournant le polygone de degré (où est le nombre de côtés) on retombe sur la même figure. Autre propriété intéressante : ils sont leur propre dual, c'est à dire que si on inverse les arêtes et les sommets alors on retombe sur la même figure :

Les exemples donnés précédemment sont tous convexes, c'est à dire vérifiant que si et sont deux points du polygone alors le segment est inclus dans le polygone, mais ce n'est pas forcément le cas. Les polygones non-convexes sont appelés « étoilés », par exemple le pentagramme est la version étoilée du pentagone.

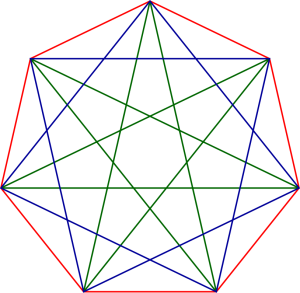
En dehors du triangle équilatéral et du carré, un polygone est nommé selon un préfixe grec donnant son nombre de côtés (penta, hexa, hepta…) et une terminaison en -gone s'il est convexe et -gramme s'il est étoilé. Ce nom caractérise bien les convexes car il n'existe qu'un seul polygone régulier convexe de côté donné, mais pas les étoilés : il peut y avoir différents polygones réguliers étoilés ayant le même nom. Par exemple, voici l'heptagone (en rouge) et les deux heptagrammes (en bleu et en vert) :

Quittons à présent le plan et passons à l'espace…

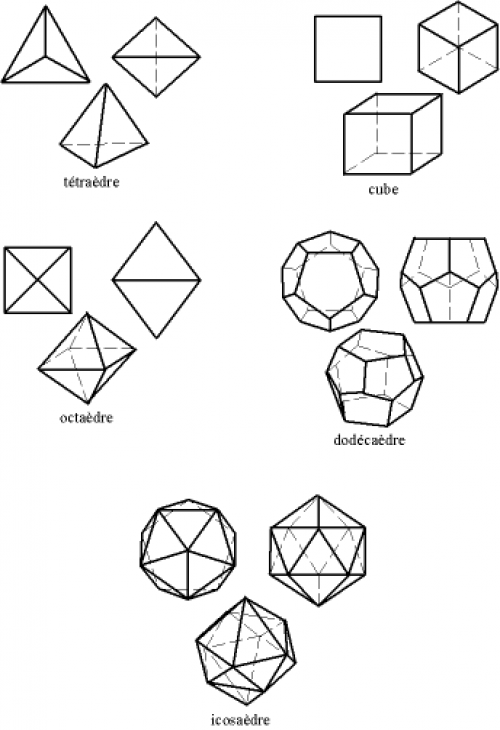
Un polyèdre (de l'espace) est dit régulier si ses faces sont régulières (des polygones réguliers) et uniformes (toutes les mêmes) et si ses sommets sont uniformes (ont le même nombre d'arêtes selon les mêmes angles). Alors qu'il existe une infinité de polygones réguliers convexes (un par nombre de côtés), il n'existe que cinq polyèdres réguliers convexes : ce sont les solides de Platon.

Les rôlistes parmi vous auront reconnu les dés classiques¹⁾ à , , , et faces. La preuve qu'il n'y a pas d'autre polyèdre régulier convexe est plutôt simple, et je trouve que Mickaël Launay de Micmaths l'a montrée de façon assez pédagogique et visuelle dans cette vidéo, donc je vous conseille d'y jeter un œil.

La notion de dualité s'applique également aux polyèdres, en échangeant les faces avec les sommets. Prenons l'exemple du cube (6 faces, 8 sommets) : chaque face est reliée à quatre autres faces, donc dans le dual du cube chaque sommet sera relié à quatre sommets, et comme chaque sommet du cube est relié à trois sommets, les faces du dual seront des triangles. Et effectivement, le dual du cube est l'octaèdre (8 faces, 6 sommets). De la même façon, le dual du dodécaèdre (12 faces, 20 sommets) est l'icosaèdre (20 faces, 12 sommets) , et le tétraèdre (4 faces, 4 sommets) est son propre dual.