Table des matières
Où nous apprenons que les carrés sont des cercles, et que 2 est au milieu entre 1 et l'infini…
Introduction
Une distance est la longueur du plus court chemin entre deux points donnés. En pratique, elle dépend du mode de transport utilisé. Par exemple une distance « à vol d'oiseau » peut ne pas être très pertinente si vous êtes en voiture et devez suivre les routes pour avancer. Ainsi, les moyens de locomotion correspondent en fait aux chemins possibles pouvant être pris : un oiseau passera par le ciel donc évitera les obstacles au sol, contrairement à un piéton qui aura besoin d'un pont. La distance pour un utilisateur correspondra donc à sa définition de l'espace. Par exemple les distances entre les étoiles ne sont pas perçues de la même façon selon que l'on ait accès ou non à l'hyperespace. Il faut donc fixer ce que l'on entend par espace.
L'espace
On repère un point dans un espace par ses coordonnées. Par exemple un GPS utilisera trois coordonnées pour nous repérer sur Terre : la latitude, la longitude et la hauteur. C'est pour cela qu'on parle d'espace à trois dimensions. Un exemple d'espace à deux dimensions est le plan, où chaque point possède une abscisse  et une ordonnée
et une ordonnée  qui le caractérisent, on parlera donc du point
qui le caractérisent, on parlera donc du point 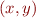 . Tout ce qui sera écrit par la suite peut être généralisé à un espace à
. Tout ce qui sera écrit par la suite peut être généralisé à un espace à  dimensions, mais dans les équations et exemples suivants je me contenterai du plan afin de mettre l'accent sur les différentes distances possibles sans que l'espace soit trop compliqué.
dimensions, mais dans les équations et exemples suivants je me contenterai du plan afin de mettre l'accent sur les différentes distances possibles sans que l'espace soit trop compliqué.
Formalisation
Mathématiquement, une distance sur un espace  est une application
est une application  , c'est à dire prenant en entrées deux points de l'espace et ayant comme sortie une valeur dans les nombres réels positifs. De plus, elle doit vérifier les trois propriétés suivantes :
, c'est à dire prenant en entrées deux points de l'espace et ayant comme sortie une valeur dans les nombres réels positifs. De plus, elle doit vérifier les trois propriétés suivantes :
- symétrie : Pour tous points
 et
et  nous avons que
nous avons que  , c'est à dire que la distance entre
, c'est à dire que la distance entre  et
et  a la même valeur que la distance entre
a la même valeur que la distance entre  et
et  .
. - séparation : Pour tous points
 et
et  nous avons que
nous avons que 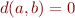 si et seulement si
si et seulement si  , c'est à dire que d'une part la distance entre un point et lui-même est nulle et d'autre part que la distance entre deux points distincts est non nulle.
, c'est à dire que d'une part la distance entre un point et lui-même est nulle et d'autre part que la distance entre deux points distincts est non nulle. - inégalité triangulaire : Pour tous points
 ,
,  et
et  nous avons que
nous avons que  , c'est à dire qu'il n'est pas possible de réduire la distance entre
, c'est à dire qu'il n'est pas possible de réduire la distance entre  et
et  en passant par un point intermédiaire
en passant par un point intermédiaire  (la distance entre
(la distance entre  et
et  est VRAIMENT la longueur du plus court chemin entre
est VRAIMENT la longueur du plus court chemin entre  et
et  ).
).
Distance entre mots
Comme toujours, si on se donne la peine de formaliser les notions d'espace et de distance, c'est parce qu'elles sont utilisables dans beaucoup de situations différentes. Par exemple, prenons comme espace l'ensemble des mots possibles avec notre alphabet, et une application  prenant en entrées deux mots et ressortant le plus petit nombre de corrections nécessaires pour passer d'un mot à l'autre. Par corrections, j'entends :
prenant en entrées deux mots et ressortant le plus petit nombre de corrections nécessaires pour passer d'un mot à l'autre. Par corrections, j'entends :
- l'insertion d'une lettre
- la suppression d'une lettre
- le remplacement d'une lettre par une autre
- l'échange de deux lettres adjacentes
Avec les trois premières corrections on obtient la distance de Levenshtein, et avec les quatre on obtient la distance de Damerau.
L'idée derrière cette application est de compter le nombre de fautes d'orthographe dans un mot, par exemple  car il faut ajouter deux lettres. Mais on peut comparer des mots n'ayant rien à voir comme
car il faut ajouter deux lettres. Mais on peut comparer des mots n'ayant rien à voir comme 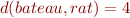 car il faut remplacer la première lettre et effacer les trois dernières.
car il faut remplacer la première lettre et effacer les trois dernières.
De façon informelle, on prouve assez rapidement que ce sont bien des distances. En effet, les corrections peuvent être inversées en une étape, ce qui permet la symétrie. Les corrections changent bien les mots, ce qui assure la séparation. Et l'inégalité triangulaire s'obtient par définition puisqu'on prend à chaque fois le plus petit nombre de corrections nécessaires.
Distances de Minkowski
Revenons à présent au plan et à des distances plus classiques. Comme précisé précédemment, les distances suivantes sont généralisables à un espace de dimension  , mais nous nous focaliserons sur le plan par souci de simplicité. Nous allons d'abord présenter différentes distances, et ensuite montrer en quoi elles font en fait partie de la même famille.
, mais nous nous focaliserons sur le plan par souci de simplicité. Nous allons d'abord présenter différentes distances, et ensuite montrer en quoi elles font en fait partie de la même famille.
Distance euclidienne
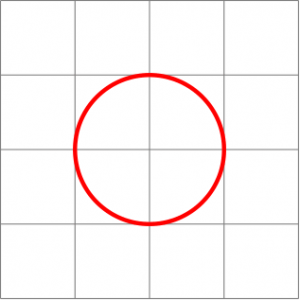
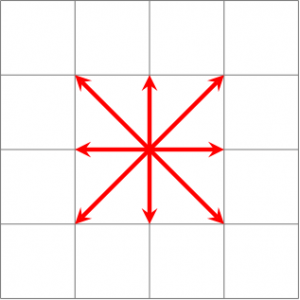
Il s'agit de la distance qui vient habituellement à l'esprit quand on parle de distance sur un plan. Pour tracer tous les points situés à même distance d'un point donné, il suffit de prendre ce point comme centre, d'ouvrir un compas avec la bonne distance, et de tracer :
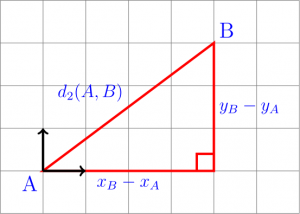
Plus formellement, la distance euclidienne (que je vais noter  pour le moment, vous verrez pourquoi plus tard ^^) entre deux points
pour le moment, vous verrez pourquoi plus tard ^^) entre deux points 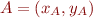 et
et 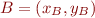 est définie par :
est définie par :

Exercice : montrer qu'il s'agit bien d'une distance (de même pour les autres ^^).
Si on récrit la définition par 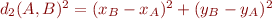 , cela devrait vous rappeler un peu le théorème de Pythagore, et pour cause :
, cela devrait vous rappeler un peu le théorème de Pythagore, et pour cause :
Ainsi, la distance euclidienne est la distance « à vol d'oiseau », mais comme annoncé il existe des distances moins classiques…
Distance de Manhattan
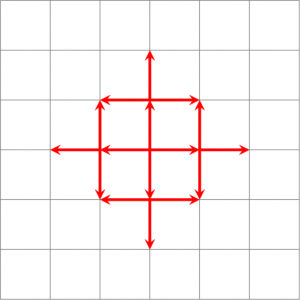
Supposons que vous soyez au volant de votre voiture / char dans une ville américaine / romaine caricaturale. Prenons par exemple une version un peu idéalisée de New-York où tous les blocs sont strictement carrés. Un pas peut se faire vers le nord, l'est, le sud ou l'ouest, et consiste à avancer vers l'intersection correspondante.
Une autre façon de le voir est de prendre le déplacement de la tour dans le jeu d'échecs. On constate dans l'exemple que si on s'intéresse aux intersections situées à deux pas de distance, on peut aller dans l'intersection située à deux pas au nord, à l'est, au sud ou à l'ouest, mais qu'il faut deux pas pour faire un pas en diagonale pour aller vers les intersections nord-est, sud-est, nord-ouest ou sud-ouest.
Remarque : Contrairement à la distance euclidienne, il n'y a pas qu'un seul chemin de plus courte distance. Par exemple pour aller à l'intersection nord-est on peut aller au nord puis à l'est, ou à l'est puis au nord. Ainsi, contrairement au plan habituel, on ne peut pas parler du plus court chemin, mais plutôt des plus courts chemins.
Formellement, la distance de Manhattan  est définie par :
est définie par :

où  est la valeur absolue du réel
est la valeur absolue du réel  , pour rappel :
, pour rappel :

La distance de Manhattan  ressemble un peu à la distance euclidienne
ressemble un peu à la distance euclidienne  , à ceci près qu'on a enlevé la racine et les carrés. Toutefois elle est bien différente. Par exemple, en prenant des
, à ceci près qu'on a enlevé la racine et les carrés. Toutefois elle est bien différente. Par exemple, en prenant des  réels et plus seulement entiers comme dans le cas de Manhattan, on peut tracer tous les points situés à distance
réels et plus seulement entiers comme dans le cas de Manhattan, on peut tracer tous les points situés à distance  du centre :
du centre :
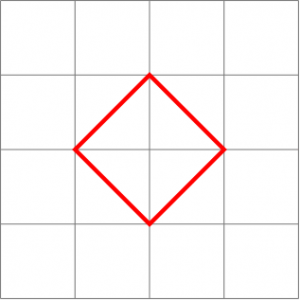
Comme dans l'exemple précédent avec les huit points cardinaux, on obtient un losange et plus un cercle. Ou pour être exact, si on définit un cercle comme l'ensemble des points situés à égale distance d'un centre donné, le cercle pour  ressemble à un losange, alors que le cercle pour
ressemble à un losange, alors que le cercle pour  est arrondi. Changer la distance a changé la forme du cercle.
est arrondi. Changer la distance a changé la forme du cercle.
Distance de Tchebychev
Cette fois nous prenons comme analogie le roi dans le jeu d'échecs : il peut se déplacer d'une case en haut, en bas, à droite, à gauche mais aussi en diagonale. La distance de Tchebychev est tout simplement le plus petit nombre de déplacements nécessaires au roi pour partir d'un point  et arriver au point
et arriver au point  .
.
Formellement, la distance de Tchebychev est définie par :
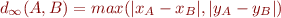
Cela peut sembler curieux de la noter  , mais tout sera révélé à la prochaine section, patience ! En attendant, l'ensemble des points situés à distance
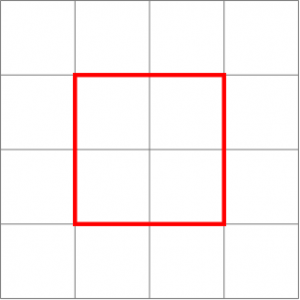
, mais tout sera révélé à la prochaine section, patience ! En attendant, l'ensemble des points situés à distance  du centre forment cette fois-ci un carré, mais maintenant il en faut plus pour vous surprendre, n'est-ce pas ?
du centre forment cette fois-ci un carré, mais maintenant il en faut plus pour vous surprendre, n'est-ce pas ?
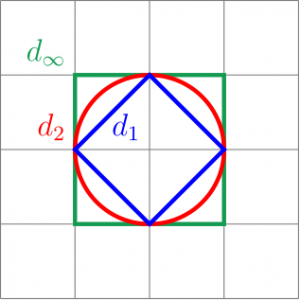
Nous allons nous contenter de ces trois distances. Avant de passer à davantage de technique, voilà un (joli, si si) dessin résumant les cercles que nous avons déjà vus :
Généralisation
A l'ordre p
J'ai appelé ces distances des « distances de Minkowski » dans la section précédente, parce qu'elles sont des généralisations de la distance de Minkowski d'ordre 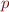 , définie par :
, définie par :
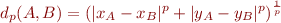
- Pour
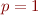 nous avons bien
nous avons bien  .
. - Pour
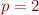 nous avons
nous avons 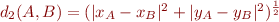 . Or
. Or 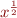 est une notation pour
est une notation pour  . Vous pouvez vous en convaincre en appliquant la formule
. Vous pouvez vous en convaincre en appliquant la formule 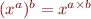 au cas
au cas 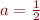 et
et  :
: 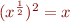 , donc pour un
, donc pour un  positif, nous avons bien que
positif, nous avons bien que 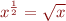 . D'où, comme la somme de deux carrés est positive,
. D'où, comme la somme de deux carrés est positive,  .
. - Pour
 … quoi ? Oui, je ne vous ai pas encore dit que
… quoi ? Oui, je ne vous ai pas encore dit que 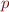 pouvait prendre ses valeurs entre
pouvait prendre ses valeurs entre  et l'infini, détail… que vaut
et l'infini, détail… que vaut  quand
quand 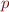 tend vers l'infini ? Et bien justement
tend vers l'infini ? Et bien justement  (à prouver ?), c'est pour cela que
(à prouver ?), c'est pour cela que  . Bon, vous vous doutez bien qu'il faudra manier ce
. Bon, vous vous doutez bien qu'il faudra manier ce  avec précaution, mais admettons.
avec précaution, mais admettons.
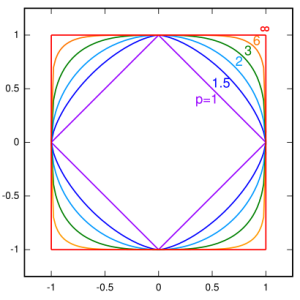
Bref, les trois distances précédentes sont bien de la même famille, et sont des exemples pour 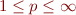 , mais on pourrait en prendre d'autres, comme
, mais on pourrait en prendre d'autres, comme 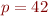 au hasard… Allez, je vous mets une jolie image de Wikipédia qui généralise mon dessin plus haut :
au hasard… Allez, je vous mets une jolie image de Wikipédia qui généralise mon dessin plus haut :
Norme
Les deux sous-sections suivantes sont un tantinet plus velues que ce qui a précédé, mais si vous êtes toujours là c'est que vous êtes courageux. Il s'agit juste d'esquisser des notions proches de celle de distance, et qui serviront pour la discussion du cas 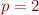 .
.
Prenons un point 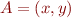 . On peut tracer le vecteur
. On peut tracer le vecteur  entre l'origine
entre l'origine 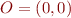 et le point
et le point  . Ce vecteur a une direction et une longueur. La norme de
. Ce vecteur a une direction et une longueur. La norme de  , notée
, notée 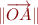 , c'est tout simplement la distance entre
, c'est tout simplement la distance entre  et
et  :
: 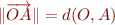 . En fait, depuis le début nous confondons le point
. En fait, depuis le début nous confondons le point  avec le vecteur
avec le vecteur 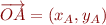 . En continuant allègrement, nous pouvons donc obtenir la norme de
. En continuant allègrement, nous pouvons donc obtenir la norme de  en fonction de la distance :
en fonction de la distance : 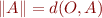 .
.
On peut bien sûr parler du vecteur  et généraliser la présentation. Comme
et généraliser la présentation. Comme 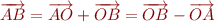 , nous avons que
, nous avons que 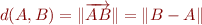 . Ainsi, nous aurions pu partir de la norme et définir la distance par
. Ainsi, nous aurions pu partir de la norme et définir la distance par 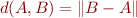 . C'est ce qui explique les
. C'est ce qui explique les  dans les définitions précédentes des distances. Ce qu'il faut retenir, c'est que les notions de distance et normes sont très proches, et qu'on peut partir de n'importe laquelle pour arriver à l'autre.
dans les définitions précédentes des distances. Ce qu'il faut retenir, c'est que les notions de distance et normes sont très proches, et qu'on peut partir de n'importe laquelle pour arriver à l'autre.
En l’occurrence, la norme d'ordre 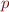 est définie par :
est définie par :
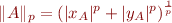
Et nous repassons bien à la distance d'ordre 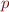 en prenant
en prenant 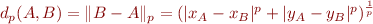 .
.
Continuité
Je vous ai dit précédemment que notre présentation était généralisable à d'autres dimensions. Par exemple, pour la distance euclidienne dans  en rajoutant la hauteur
en rajoutant la hauteur  nous passerions de
nous passerions de  à
à  . Nous pouvons le faire sans problème pour n'importe quel nombre de dimension, que ce soit pour la distance ou la norme. Mais… et pour une infinité de dimensions ?
. Nous pouvons le faire sans problème pour n'importe quel nombre de dimension, que ce soit pour la distance ou la norme. Mais… et pour une infinité de dimensions ?
En prenant un point 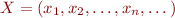 nous pourrions définir la norme de
nous pourrions définir la norme de  par :
par :
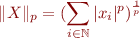
En faisant tendre  vers l'infini nous aurions bien sûr des problèmes de convergence, mais ce n'est pas le plus intéressant. Ici nous avons défini un point en associant une coordonnée
vers l'infini nous aurions bien sûr des problèmes de convergence, mais ce n'est pas le plus intéressant. Ici nous avons défini un point en associant une coordonnée  à chaque numéro
à chaque numéro  de dimension, mais nous pourrions généraliser cela en définissant un point par une fonction
de dimension, mais nous pourrions généraliser cela en définissant un point par une fonction 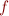 qui prendrait ses valeurs par exemple dans les réels et plus dans les entiers:
qui prendrait ses valeurs par exemple dans les réels et plus dans les entiers:
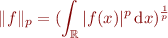
C'est le successeur direct de la distance de Minkowski d'ordre 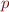 : on a « juste » remplacé la somme discrète
: on a « juste » remplacé la somme discrète  par la somme continue
par la somme continue  , et la coordonnée
, et la coordonnée  dépendant de
dépendant de  par un
par un 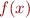 dépendant de
dépendant de  . Et notre point n'est plus une liste de coordonnées mais une fonction
. Et notre point n'est plus une liste de coordonnées mais une fonction 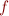 .
.
Bien sûr, comme il s'agit d'une somme infinie, il y a BEAUCOUP de fonctions 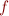 pour lesquelles
pour lesquelles  . Nous nous intéressons à l'ensemble des fonctions
. Nous nous intéressons à l'ensemble des fonctions 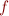 telles que
telles que 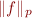 soit fini, et nous notons
soit fini, et nous notons  cet espace de fonctions. Par exemple, en violant davantage la notion de cercle, on pourrait dire que le cercle de rayon
cet espace de fonctions. Par exemple, en violant davantage la notion de cercle, on pourrait dire que le cercle de rayon  dans
dans  est l'ensemble des fonctions
est l'ensemble des fonctions 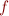 telles que
telles que 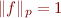 .
.
Le cas p = 2
Bon, on va se calmer un peu et revenir sur les distances de Minkowski d'ordre 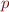 , histoire de finir un peu plus en douceur. Je vous ai dit au début que la distance euclidienne « à vol d'oiseau » est celle qui vient la première à l'esprit, et je voulais donc vous dire en quoi
, histoire de finir un peu plus en douceur. Je vous ai dit au début que la distance euclidienne « à vol d'oiseau » est celle qui vient la première à l'esprit, et je voulais donc vous dire en quoi  est spéciale.
est spéciale.
Au sujet des espace  il y a un résultat assez important appelé l'inégalité de Hölder, qui montre que pour deux nombres
il y a un résultat assez important appelé l'inégalité de Hölder, qui montre que pour deux nombres 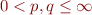 vérifiant
vérifiant 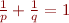 si
si 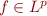 et
et  alors le produit
alors le produit 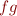 de
de 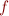 et de
et de  vérifie
vérifie 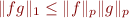 , donc est dans
, donc est dans  .
.
Si vous avez le sens du détail, vous aurez remarqué que je parle ici d'un nombre 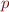 entre
entre  et l'infini, alors que dans la définition des distances de Minkowski je parlais d'un
et l'infini, alors que dans la définition des distances de Minkowski je parlais d'un 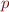 entre
entre  et l'infini… alors ? Oh, c'est juste que cette inégalité est valide aussi pour
et l'infini… alors ? Oh, c'est juste que cette inégalité est valide aussi pour 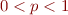 , mais que dans ce cas
, mais que dans ce cas  ne vérifie plus l'inégalité triangulaire donc n'est plus une distance.
ne vérifie plus l'inégalité triangulaire donc n'est plus une distance.
Bon, c'est assez compliqué, mais je voulais surtout attirer votre attention sur la condition 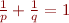 . D'ailleurs pour
. D'ailleurs pour 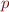 et
et  la vérifiant on peut montrer en utilisant l'inégalité de Hölder qu'en un sens (de dualité topologique, si vous voulez VRAIMENT tout savoir)
la vérifiant on peut montrer en utilisant l'inégalité de Hölder qu'en un sens (de dualité topologique, si vous voulez VRAIMENT tout savoir)  et
et  sont des reflets l'un de l'autre. Pour avoir une joli symétrie il faut donc que
sont des reflets l'un de l'autre. Pour avoir une joli symétrie il faut donc que  soit son propre reflet. Dans ce cas nous avons
soit son propre reflet. Dans ce cas nous avons 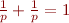 , donc
, donc 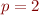 , et oui !
, et oui !
C'est pour cela qu'en un sens  est exactement la distance « médiane » entre
est exactement la distance « médiane » entre  et
et  (ce qui se voit bien sur le dessin, je trouve), qui sont elles-mêmes les extrémités des distances de Minkowski. Certes, il y a d'autres distances (par exemple la distance entre deux mots), mais ce sont les distances de Minkowski que nous utilisons dans les espaces usuels (le plan, l'espace, etc.). Personnellement, je trouve assez formidable qu'une distance dérivant de quelque chose d'aussi simple et ancien que le théorème de Pythagore ait une place aussi privilégiée parmi les espaces de fonctions compliqués que nous étudions de nos jours…
(ce qui se voit bien sur le dessin, je trouve), qui sont elles-mêmes les extrémités des distances de Minkowski. Certes, il y a d'autres distances (par exemple la distance entre deux mots), mais ce sont les distances de Minkowski que nous utilisons dans les espaces usuels (le plan, l'espace, etc.). Personnellement, je trouve assez formidable qu'une distance dérivant de quelque chose d'aussi simple et ancien que le théorème de Pythagore ait une place aussi privilégiée parmi les espaces de fonctions compliqués que nous étudions de nos jours…
Note : J'applique le cas p = 2 dans mon article de conception sur les distances dans Nova. Et en passant voici un article intéressant sur le pavage hexagonal.
Petit note : cette vidéo de Science4All évoque aussi le fait que les fonctions 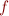 telles que
telles que 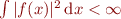 sont celles qui sont égales à leur série de Fourier…
sont celles qui sont égales à leur série de Fourier…